“Fidelius示例教程”的版本间差异
跳到导航
跳到搜索
| 第52行: | 第52行: | ||
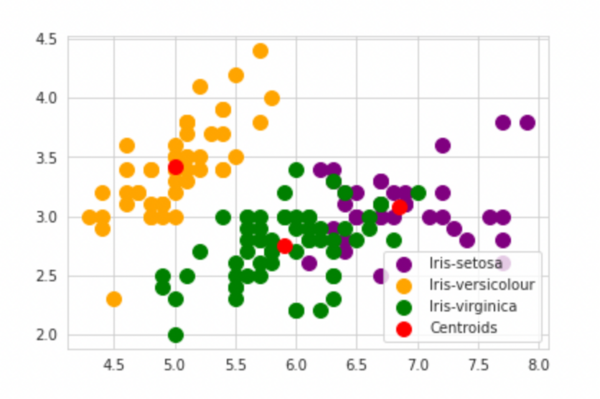
== K-Means聚类算法 == | == K-Means聚类算法 == | ||
聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程,聚类就是一种发现这种内在结构的技术,聚类技术经常被称为无监督学习。 | |||
k均值聚类(K-Means)是最著名的划分聚类算法,由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k,k由用户指定,k均值算法根据某个距离函数反复把数据分入k个聚类中。 | |||
[[文件:kmeans.png|600px|center]] | [[文件:kmeans.png|600px|center]] | ||
2022年5月12日 (四) 07:27的版本
您可以通过本页面了解如何在Fidelius中运行一个示例程序。
基于Iris数据集的K-Means聚类算法
基于Iris数据集的K-Means聚类是机器学习中一个非常经典的学习示例,这里我们介绍一下如何在Fidelius中实现这个例子。
Iris鸢尾花数据集
Iris 鸢尾花数据集内包含 3 类分别为山鸢尾(Iris-setosa)、变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica),共 150 条记录,每类各 50 个数据,每条记录都有 4 项特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度。
- sepallength:萼片长度
- sepalwidth:萼片宽度
- petallength:花瓣长度
- petalwidth:花瓣宽度
以上四个特征的单位都是厘米(cm)
Iris数据集部分展示如下:
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | Iris-setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | Iris-setosa |
| 5 | 5.4 | 3.9 | 1.7 | 0.4 | Iris-setosa |
| 6 | 4.6 | 3.4 | 1.4 | 0.3 | Iris-setosa |
| 7 | 5.0 | 3.4 | 1.5 | 0.2 | Iris-setosa |
| 8 | 4.4 | 2.9 | 1.4 | 0.2 | Iris-setosa |
| 9 | 4.9 | 3.1 | 1.5 | 0.1 | Iris-setosa |
K-Means聚类算法
聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程,聚类就是一种发现这种内在结构的技术,聚类技术经常被称为无监督学习。
k均值聚类(K-Means)是最著名的划分聚类算法,由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k,k由用户指定,k均值算法根据某个距离函数反复把数据分入k个聚类中。