“Fidelius示例教程”的版本间差异
ChenminWang(讨论 | 贡献) |
|||
| (未显示3个用户的25个中间版本) | |||
| 第1行: | 第1行: | ||
您可以通过本页面了解如何在 Fidelius 中运行一个示例程序。 | |||
= | = 基于 Iris 数据集的 K-Means 聚类算法 = | ||
基于 Iris 数据集的 K-Means 聚类是机器学习中一个非常经典的学习示例,这里我们介绍一下如何在 Fidelius 中实现这个例子。 | |||
== Iris 鸢尾花数据集 == | |||
Iris 鸢尾花数据集内包含 3 类鸢尾花,分别为山鸢尾(Iris-setosa)、变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica),共 150 条记录,每类各 50 个数据,每条记录都有 4 项特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度。 | |||
*sepallength:萼片长度 | |||
*sepalwidth:萼片宽度 | |||
*petallength:花瓣长度 | |||
*petalwidth:花瓣宽度 | |||
以上四个特征的单位都是厘米(cm) | |||
[[文件:Iris pic.15.png|600px|center]] | [[文件:Iris pic.15.png|600px|center]] | ||
Iris数据集部分展示如下: | |||
{| class="wikitable" | |||
|+ | |||
|- | |||
! !! sepal_length !! sepal_width !! petal_length !! petal_width !! species | |||
|- | |||
| 0 || 5.1 || 3.5 || 1.4 || 0.2 || Iris-setosa | |||
|- | |||
| 1 || 4.9 || 3.0 || 1.4 || 0.2 || Iris-setosa | |||
|- | |||
| 2 || 4.7 || 3.2 || 1.3 || 0.2 || Iris-setosa | |||
|- | |||
| 3 || 4.6 || 3.1 || 1.5 || 0.2 || Iris-setosa | |||
|- | |||
| 4 || 5.0 || 3.6 || 1.4 || 0.2 || Iris-setosa | |||
|- | |||
| 5 || 5.4 || 3.9 || 1.7 || 0.4 || Iris-setosa | |||
|- | |||
| 6 || 4.6 || 3.4 || 1.4 || 0.3 || Iris-setosa | |||
|- | |||
| 7 || 5.0 || 3.4 || 1.5 || 0.2 || Iris-setosa | |||
|- | |||
| 8 || 4.4 || 2.9 || 1.4 || 0.2 || Iris-setosa | |||
|- | |||
| 9 || 4.9 || 3.1 || 1.5 || 0.1 || Iris-setosa | |||
|} | |||
== K-Means 聚类算法 == | |||
K 均值聚类(K-Means)是最著名的划分聚类算法,简洁和高效使得他成为所有聚类算法中最广泛使用的。其认为两个目标的距离越近,其相似度越大。 | |||
算法步骤: | |||
# 选择初始化的 k 个样本作为初始聚类中心 a = a<sub>1</sub>, a<sub>2</sub>, ... a<sub>k</sub>; | |||
# 针对数据集中每个样本 x<sub>i</sub> 计算它 k 个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中; | |||
# 针对每个类别 a<sub>j</sub>,重新计算它的聚类中心,即属于该类的所有样本的质心; | |||
# 重复上面 2 3 两步操作,直到达到某个中止条件(迭代次数、最小误差变化等)。 | |||
K-Means算法通常使⽤肘部法则来选择 K 值。肘部法则考察聚类后全体样本的误差平⽅和 SSE,将 SSE 随 K 值的变化由快速下降转变为缓慢变化的拐点处的 K 值,作为最佳聚类簇数。 | |||
肘部法则选择 K 值的依据:随着聚类数 K 的增⼤,样本划分会更加精细,每个簇的聚合程度会逐渐提⾼,那么误差平⽅和 SSE ⾃然会逐渐变⼩。且当 K ⼩于真实聚类数时,K 的增⼤会⼤幅增加每个簇的聚合程度,故 SSE 的下降幅度会很⼤;当 K 达到真实聚类数时,再增加 K 所得到的聚合程度,回报就会迅速变⼩,所以 SSE 的下降幅度会骤减,然后随着K值的继续增⼤⽽趋于平缓。也就是说 SSE 与 K 之间的关系就像⼿肘的形状,这个肘部对应的K值就是数据的真实聚类数。 | |||
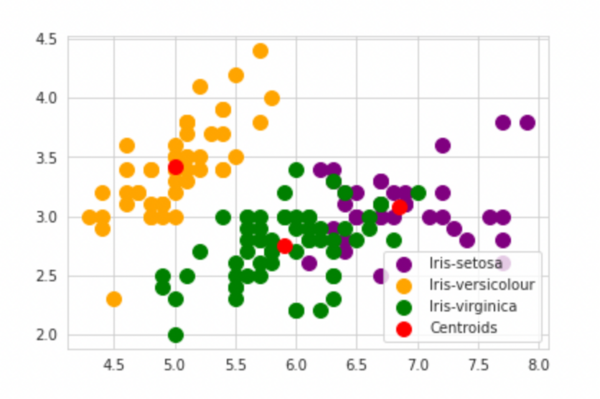
使⽤K-Means对数据集iris进⾏聚类分析:加载iris数据集,按照4个特征,使⽤肘部法则确定最佳的K值,然后使⽤KMeans类进⾏聚类,最后可视化聚类结果。 | |||
[[文件:kmeans.png|600px|center]] | |||
== 在 Fidelius 中运行 K-Means == | |||
0. 确保Fidelius已经安装完成,可通过源码方式安装,或APT的方式安装,安装教程可参考[https://doc-dianshu.yeez.tech/index.php?title=Fidelius%E9%83%A8%E7%BD%B2%E6%95%99%E7%A8%8B#%E5%AE%89%E8%A3%85_Fidelius 安装Fidelius] | |||
1. 下载示例代码 | |||
$ git clone https://github.com/YeeZTech/YPC-algo-example.git | |||
2. 编译示例代码 | |||
$ cd YPC-algo-example && mkdir -p build && cd build | |||
$ cmake -DCMAKE_PREFIX_PATH=$YPC_INSTALL_DIR/lib/cmake -DCMAKE_BUILD_TYPE=RelWithDebInfo .. | |||
$ make -j8 | |||
注意: $YPC_INSTALL_DIR 为 Fidelius 的安装路径,例如通过APT的方式安装后,其默认路径为 /opt/ypc | |||
3. 运行示例代码 | |||
$ cd YPC-algo-example/integrate | |||
$ python3 test_iris.py | |||
2023年3月24日 (五) 03:22的最新版本
您可以通过本页面了解如何在 Fidelius 中运行一个示例程序。
基于 Iris 数据集的 K-Means 聚类算法
基于 Iris 数据集的 K-Means 聚类是机器学习中一个非常经典的学习示例,这里我们介绍一下如何在 Fidelius 中实现这个例子。
Iris 鸢尾花数据集
Iris 鸢尾花数据集内包含 3 类鸢尾花,分别为山鸢尾(Iris-setosa)、变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica),共 150 条记录,每类各 50 个数据,每条记录都有 4 项特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度。
- sepallength:萼片长度
- sepalwidth:萼片宽度
- petallength:花瓣长度
- petalwidth:花瓣宽度
以上四个特征的单位都是厘米(cm)
Iris数据集部分展示如下:
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | Iris-setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | Iris-setosa |
| 5 | 5.4 | 3.9 | 1.7 | 0.4 | Iris-setosa |
| 6 | 4.6 | 3.4 | 1.4 | 0.3 | Iris-setosa |
| 7 | 5.0 | 3.4 | 1.5 | 0.2 | Iris-setosa |
| 8 | 4.4 | 2.9 | 1.4 | 0.2 | Iris-setosa |
| 9 | 4.9 | 3.1 | 1.5 | 0.1 | Iris-setosa |
K-Means 聚类算法
K 均值聚类(K-Means)是最著名的划分聚类算法,简洁和高效使得他成为所有聚类算法中最广泛使用的。其认为两个目标的距离越近,其相似度越大。
算法步骤:
- 选择初始化的 k 个样本作为初始聚类中心 a = a1, a2, ... ak;
- 针对数据集中每个样本 xi 计算它 k 个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中;
- 针对每个类别 aj,重新计算它的聚类中心,即属于该类的所有样本的质心;
- 重复上面 2 3 两步操作,直到达到某个中止条件(迭代次数、最小误差变化等)。
K-Means算法通常使⽤肘部法则来选择 K 值。肘部法则考察聚类后全体样本的误差平⽅和 SSE,将 SSE 随 K 值的变化由快速下降转变为缓慢变化的拐点处的 K 值,作为最佳聚类簇数。
肘部法则选择 K 值的依据:随着聚类数 K 的增⼤,样本划分会更加精细,每个簇的聚合程度会逐渐提⾼,那么误差平⽅和 SSE ⾃然会逐渐变⼩。且当 K ⼩于真实聚类数时,K 的增⼤会⼤幅增加每个簇的聚合程度,故 SSE 的下降幅度会很⼤;当 K 达到真实聚类数时,再增加 K 所得到的聚合程度,回报就会迅速变⼩,所以 SSE 的下降幅度会骤减,然后随着K值的继续增⼤⽽趋于平缓。也就是说 SSE 与 K 之间的关系就像⼿肘的形状,这个肘部对应的K值就是数据的真实聚类数。
使⽤K-Means对数据集iris进⾏聚类分析:加载iris数据集,按照4个特征,使⽤肘部法则确定最佳的K值,然后使⽤KMeans类进⾏聚类,最后可视化聚类结果。
在 Fidelius 中运行 K-Means
0. 确保Fidelius已经安装完成,可通过源码方式安装,或APT的方式安装,安装教程可参考安装Fidelius
1. 下载示例代码
$ git clone https://github.com/YeeZTech/YPC-algo-example.git
2. 编译示例代码
$ cd YPC-algo-example && mkdir -p build && cd build $ cmake -DCMAKE_PREFIX_PATH=$YPC_INSTALL_DIR/lib/cmake -DCMAKE_BUILD_TYPE=RelWithDebInfo .. $ make -j8
注意: $YPC_INSTALL_DIR 为 Fidelius 的安装路径,例如通过APT的方式安装后,其默认路径为 /opt/ypc
3. 运行示例代码
$ cd YPC-algo-example/integrate $ python3 test_iris.py